Diferença chave: As ondas seno e cosseno são formas de onda de sinal que são idênticas entre si. A principal diferença entre os dois é que a onda cosseno leva a onda senoidal em uma quantidade de 90 graus.

Uma onda senoidal descreve uma mudança ou movimento recorrente. Ela é conhecida como onda senoidal, pois tem a forma semelhante à função seno, quando é plotada em um gráfico. O gráfico mostra a repetição de um segmento de onda de maneira repetida. A função seno é geralmente denotada por f (x) = a sin (bx + c) + d.

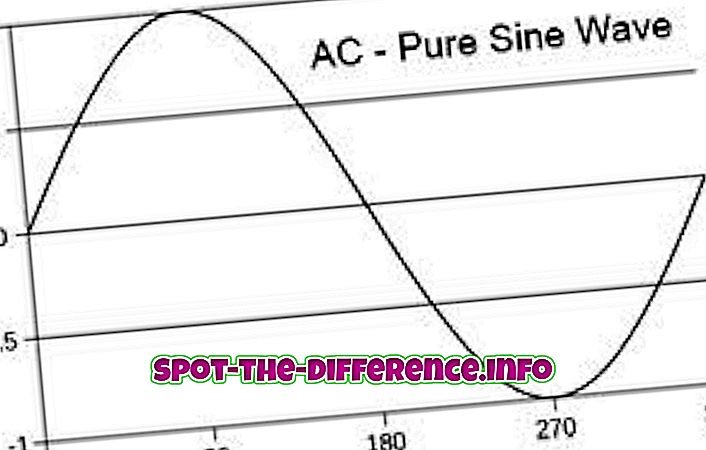
Onde, a, b, c e d são todas constantes, com a não é igual a zero

x é medido em radianos

A função pode ser simplesmente referida como f (x) = sin (x), quando a = b = 1 e c = d = 0

Também pode ser escrito na forma de f (t) = A sen (2 πωt + ϕ), onde A = amplitude, ω = frequência e ϕ = fase ou deslocamento.

A onda cosseno é semelhante a uma função cosseno quando representada em um gráfico. É preciso saber que as ondas senoidais e cosseno são silenciosas. Pode-se notar facilmente que toda função cosseno é basicamente uma função senoidal deslocada. A função cosseno é movida para a esquerda por uma quantidade de π / 2.

A equação de uma função cosseno é dada por f (x) = a cos (bx + c) + d, onde, a, b, c e d são todas constantes com a não é igual a zero.

x é medido em radianos (π radianos = 180 graus, o ângulo medido de um semicírculo)

Portanto, a função cosseno e a função senoidal são idênticas uma à outra, exceto com o deslocamento horizontal à esquerda de π / 2 radianos na função cosseno. Devido a essa semelhança, qualquer função cosseno pode ser escrita em termos de uma função seno como cos x = sin (x + π / 2). Também não há diferença na freqüência de um cosseno e sua onda senoidal correspondente. Ambos têm um máximo de 1 e um mínimo de -1. Estatística de curva de função senoidal em 0 e, em seguida, move-se para cima para 1 por π / 2 radianos e, em seguida, volta para -1. Por outro lado, a curva cosseno começa em 1, desce até π radianos e depois se move novamente para cima.

Comparação entre Sine e Cosine Wave:

	Onda senoidal	Cosine Wave
Definição	Representa uma curva matemática que descreve um movimento de oscilação repetitivo semelhante a uma função senoidal	Representa uma curva matemática que descreve um movimento de oscilação repetitivo semelhante a uma função cosseno
Fórmula simples para representação	f (x) = sin (x)	f (x) = cos (x)
Movimento	Estatística da curva de função senoidal em 0 e, em seguida, move-se para cima para 1 por π / 2 radianos e, em seguida, volta para -1	a curva cosseno começa em 1, desce até π radianos e, em seguida, novamente se move para cima
Exemplo	Em circuitos de corrente alternada (CA), a tensão oscila em um padrão de onda senoidal	Ondas na superfície do mar são ondas cosseno simples.
Tipo	Funções ímpares	Até funções
Outro nome	Sinusóide	Senoidal como cos (x) = seno (x + π / 2)