Diferença chave: Uma parábola é uma seção cônica que é criada quando um plano corta uma superfície cônica paralela ao lado do cone. Uma hipérbole é criada quando um plano corta uma superfície cônica paralela ao eixo.

Parábola e hipérbole são duas palavras, seções e equações diferentes usadas na matemática para descrever duas seções diferentes de um cone. Estes são diferentes em forma, tamanho e vários outros fatores incluindo fórmulas que são usadas para calculá-lo. Para compreendê-los, vamos primeiro entender o cone e as diferentes seções cônicas.

Uma seção cônica é uma curva que é obtida quando um plano se cruza com um cone de várias maneiras diferentes. Os cortes obtidos da interseção incluem elipse, círculo, parábola e hipérbole. De acordo com a geometria analítica, a cônica é definida como “uma curva algébrica plana de grau 2”. A definição popular de seção cônica inclui um ponto de foco, linha diretriz e excentricidade. Espera-se que o ponto de foco e as linhas da diretriz estejam em uma ração fixa em uma cônica. A relação é conhecida como a excentricidade da seção cônica. A excentricidade das elipses, parábolas e hipérboles difere; as elipses têm uma excentricidade menor que 1, as parábolas têm uma excentricidade igual a 1 e as hipérboles têm uma excentricidade maior que 1. O mais antigo trabalho conhecido em seções cônicas pode ser datado do século IV aC por Menaechmus, que descobriu uma maneira para resolver o problema de dobrar o cubo através do uso de parábola.

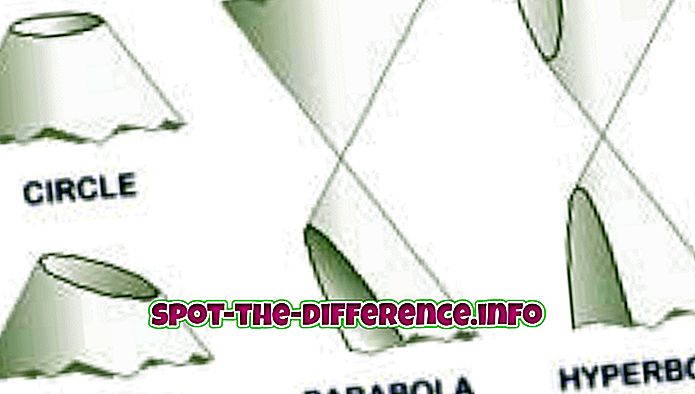
Uma parábola é uma seção cônica que é criada quando um avião se cruza com um cone. Parábolas ou parábolas formam-se a partir da interseção de uma superfície cônica circular direita e um plano paralelo a uma linha reta geradora daquela superfície. Outra maneira de criar uma parábola é quando um locus de pontos em um plano equidistante do foco e da diretriz cria uma parábola. Na álgebra, as parábolas são comumente usadas em gráficos de funções quadráticas, usando a fórmula y = x ^ 2.

Uma linha que divide a parábola pelo meio é conhecida como o eixo de simetria; esta linha também é perpendicular à diretriz e passa pelo foco. Os pontos que estão no eixo de simetria que cruzam a parábola são chamados de 'vértice'. A distância entre o vértice e o foco é conhecida como 'distância focal'. Parábolas podem abrir em qualquer direção, incluindo para cima, baixo, direita ou esquerda. Também uma característica principal das parábolas é que elas são todas iguais, diferindo apenas em tamanho. Eles podem ser reposicionados e redimensionados exatamente para se adaptarem a qualquer outra parábola. As parábolas são usadas em várias aplicações, como refletores de farol de automóvel, projeto de mísseis balísticos, etc. Eles também desempenham um papel importante na física, engenharia, matemática, etc.

As hipérboles são uma curva suave que ocorre quando um plano cruza com o cone paralelo ao eixo y que cria um corte ao longo do lado do cone. Uma hipérbole é definida por suas propriedades geométricas ou equações para as quais é um conjunto de soluções. O termo "hipérbole" é derivado da palavra grega que significa "over-thrown" ou "excessivo". Acredita-se que o termo seja cunhado por Apolônio de Perga, que contribuiu enormemente para o estudo das seções cônicas.

Sabe-se que uma hipérbole tem ramificações que são imagens espelhadas entre si e se assemelham a dois arcos infinitos. Os pontos nos dois ramos que estão mais próximos uns dos outros são chamados de vértices. A linha que conecta os vértices é conhecida como eixo transversal ou eixo maior, que corresponde ao diâmetro maior de uma elipse. O ponto médio de um eixo transversal é conhecido como o centro da hipérbole. A equação de uma hipérbole é escrita como x2 / a2-y2 / b2 = 1. As hipérboles são usadas em várias aplicações no mundo de hoje, incluindo o caminho seguido pela sombra da ponta de um relógio de sol, a forma de uma órbita aberta; é usado como um arco em muitos edifícios construídos, como equações em matemática e geometria, física, etc.

Hipérboles e parábolas são curvas abertas, o que significa que elas não terminam e continuam indefinidamente até o infinito, algo que elipses e círculos não podem fazer.