Diferença chave: Um círculo e uma elipse fecharam formas curvas. Em um círculo, todos os pontos estão igualmente distantes do centro, o que não é o caso de uma elipse; em uma elipse, todos os pontos estão em distâncias diferentes do centro.
Matematicamente, um círculo é uma forma importante no campo da geometria e seus estados de definição: um círculo é uma forma com todos os pontos na mesma distância do seu centro. É nomeado pelo seu centro. Alguns exemplos do mundo real de um círculo são rodas, um prato de jantar e (a superfície de) uma moeda.
A palavra " circo " é derivada do termo grego " kirkos ", que é uma metátese do grego homérico e significa " aro " ou " anel ". O círculo é conhecido antes da história registrada. O Sol e a Lua são exemplos naturais de um círculo, ao passo que, mesmo um pequeno talo soprando ao vento, forma a forma de um círculo na areia. O princípio de um círculo foi aplicado na formação de rodas e engrenagens pelo homem pré-histórico. Agora, na era moderna, existem inúmeras variedades de máquinas baseadas na forma circular. O estudo de um círculo e seu desenvolvimento é aplicável nos campos da matemática, geometria, astronomia e cálculo.
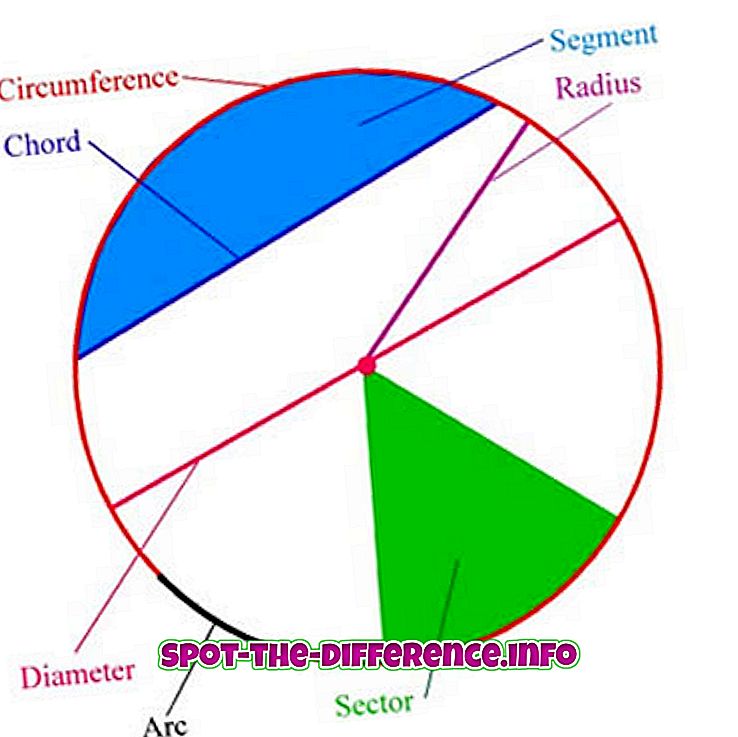
Os seguintes termos estão envolvidos na terminologia do círculo:
Arco : qualquer parte conectada do círculo.
Centro : o ponto equidistante dos pontos no círculo.
Raio : um segmento de linha que une o centro do círculo a qualquer ponto no próprio círculo; ou o comprimento de tal segmento, que é meio diâmetro.
Diâmetro : um segmento de linha cujos pontos finais estão no círculo e que passa pelo centro; ou o comprimento de tal segmento de linha, que é a maior distância entre quaisquer dois pontos no círculo. É um caso especial de um acorde, ou seja, o acorde mais longo, e é o dobro do raio.
Circunferência e: o comprimento de um circuito ao longo do círculo.
Chord : um segmento de linha cujos pontos finais estão no círculo.
Tangente : uma linha reta coplanar que toca o círculo em um único ponto.
Semicírculo : uma região limitada por um diâmetro e um arco entre os pontos finais do diâmetro. É um caso especial de um segmento circular, ou seja, o maior.
Setor circular : uma região delimitada por dois raios e um arco entre os raios.
Matematicamente, uma elipse é uma forma comum no campo da matemática. Sua definição afirma: uma linha curva formando um circuito fechado, onde a soma das distâncias de dois pontos (focos) para cada ponto da linha é constante. Os exemplos da vida real de uma elipse são: um bambolê, um copo de água e um simples prato de jantar quando inclinados para ver em um ângulo.
Apolônio de Perga deu o nome de "elipse" em suas cônicas, que enfatiza a conexão de uma curva com a aplicação de áreas. É uma curva em um plano em torno de dois pontos focais, de tal forma que uma linha reta traçada de um dos pontos focais para qualquer ponto da curva e depois de volta para o outro ponto focal tem o mesmo comprimento para cada ponto da curva. Sua forma é representada por sua excentricidade, que é arbitrariamente próxima de 1. O estudo da elipse e suas propriedades são comumente aplicáveis no campo da física, astronomia e engenharia. As órbitas dos planetas com o Sol em um dos pontos focais, as luas orbitando os planetas e outros sistemas tendo dois corpos astronômicos são os exemplos gerais de caminhos elípticos. A forma dos planetas e das estrelas costuma ser bem descrita pelos elipsóides. A elipse também é considerada a figura mais simples de Lissajous, formada quando os movimentos horizontal e vertical são sinusóides com a mesma frequência.
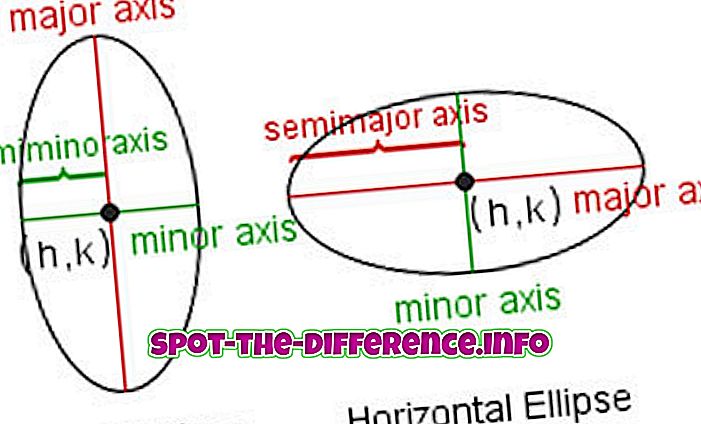
Os termos envolvidos principalmente na terminologia da elipse são:
Foco : A distância do centro e é expressa em termos dos raios maior e menor.
Excentricidade : A excentricidade da elipse (comumente denotada como e ou ε) é expressa em termos usando o fator de achatamento.
Directrix : é uma linha paralela ao eixo menor, e com a qual cada foco está associado.
Latus rectum : Os acordes de uma elipse que são perpendiculares ao eixo maior e passam por um dos seus focos são chamados de latus rectum da elipse.
Eixo principal / menor : os diâmetros mais longos e mais curtos de uma elipse. O comprimento do eixo maior é igual à soma das duas linhas geradoras.
Semi-major / Semi-minor axis : A distância do centro até o ponto mais distante e mais próximo da elipse. Metade do eixo maior / menor.
Acordes : Os pontos médios de um conjunto de acordes paralelos de uma elipse são colineares.
Circunferência : está associada ao comprimento do semi-eixo maior e à excentricidade e é parte integrante de uma elipse.
Comparação entre Circle e Ellipse:
Círculo | Elipse | |
Definições | Um círculo é uma figura de plano redondo cujo limite (a circunferência) consiste de pontos equidistantes de um ponto fixo (o centro). | Uma elipse é uma forma oval regular, traçada por um ponto que se move em um plano de modo que a soma de suas distâncias de dois outros pontos (os focos) é constante, ou é resultado quando um cone é cortado por um plano oblíquo, o que não cruze a base. |
Variações | Os círculos não variam em forma; eles permanecem da mesma forma, mesmo quando a visão é alterada. | As elipses variam de forma muito ampla e plana a quase circular, dependendo da distância entre os focos. |
Consistência do raio | Tem um raio constante em toda a forma. | Não tem um raio constante em toda a forma. |
Componentes principais | O círculo tem um raio, que fica no centro. | Elipse tem dois focos, que estão nas duas extremidades. |
Área | π × r ^ 2 Onde 'r' é o raio do círculo. | π × a × b Onde 'a' é o comprimento do semi-eixo principal, e 'b' é o comprimento do eixo semi-menor. |
Equações padrão | (xa) ^ 2 + (yb) ^ 2 = r ^ 2 | x ^ 2 / a ^ 2 + y ^ 2 / b ^ 2 = 1 |
Semelhança | Os círculos são as formas exclusivas, das quais as outras formas se originam. | Elipses também surgem como imagens de um círculo sob projeção paralela e os casos limitados de projeção em perspectiva. |